高考必考的数学公式
高考必考的数学公式
高考考试,在数学这门科目上必然离不开数学公式的应用,下面是学习啦小编给大家带来的高考必考的数学公式,希望对你有帮助。
高考必考的数学公式(一)
积化和差计算公式
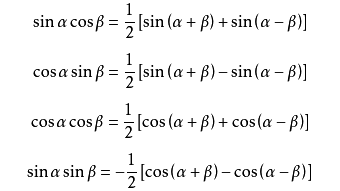
高等三角函数公式
asinx+bcosx=√(a²+b²)sin[x+\arctan(b/a)]。(a>0)

高考必考的数学公式(二)
函数求导公式 (1)设y=c(常数),则y'=0
因为y=c的图象是平行于x轴的直线,其上任一点的切线即为直线本身,所以切线的斜率都是0.此公式可叙述成“常数函数的导数为零”
(2)(xn)'=nxn-1(n为正整数)
正整数幂函数的导数等于幂指数n与自变量的(n-1)次幂的乘积
(3)(sinx)'=cosx
正弦函数的导数等于余弦函数
(4)(cosx)'=-sinx
余弦函数的导数等于正弦函数前面添一个负号
三角函数诱导公式之常用公式 公式本质:所谓三角函数诱导公式,就是将角n・(π/2)±α的三角函数转化为角α的三角函数。
常用公式
公式一:设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα k∈z
cos(2kπ+α)=cosα k∈z
tan(2kπ+α)=tanα k∈z
cot(2kπ+α)=cotα k∈z
公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
公式三:任意角α与 -α的三角函数值之间的关系:
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:π/2±α与α的三角函数值之间的关系:
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
推算公式:3π/2±α与α的三角函数值之间的关系:
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
看了“高考必考的数学公式”的人还看了:
